磁石の吸引力と反発力の比較実験
永久磁石と電磁石で実験しました。電磁石の場合は交流と直流で実験しました。磁石と磁石間の距離を変えて実験しました。交流と直流は殆ど同じでした。永久磁石でも電磁石でも磁石間の距離が短いほど、吸引力に対する反発力の比率は小さくなりました。永久磁石の場合は、磁石間の距離が磁石の大きさ以上になると吸引力と反発力がほぼ同じになりました。電磁石の場合は、磁石間の距離が磁石の大きさでの反発力の比率は
55%でした。
1.永久磁石の場合の吸引力と反発力の比較実験
(1)実験概略配置図

(2)ドーナツ型永久磁石の場合
ドーナツ型永久磁石 外形:28mm 内径:10mm 厚さ:3.5mm
磁石の水平位置の変化で吸引力、反発力の値が少し変わりました。
実験結果
隙間 :約2mm

(3)上の磁石と下の磁石の大きさを変えた実験1
上の磁石の寸法(円板) 外形:29mm 厚さ:4mm
下の磁石寸法 (円板) 外形:20mm 厚さ:3mm
隙間 :約2mm

(4)上の磁石と下の磁石の大きさを変えた実験2
上の磁石の寸法(円板) 外形:40mm 厚さ:4mm
下の磁石寸法 (円板) 外形:20mm 厚さ:4mm
隙間 :約20mm
磁石の種類:ネオジウム

(5)上の磁石と下の磁石の隙間を変えた実験
上の磁石の寸法(円板 ネジオウム) 外形:40mm 厚さ:4mm
下の磁石寸法 (円板 ) 外形:20mm 厚さ:3mm
実験結果

反発力の場合は、隙間が狭くなると、上の磁力線と下の磁力線の打ち消し合い
が起こり、反発力が小さくなるものと考えています。
(6)U字永久磁石


2.電磁石での吸引力と反発力の比較実験
(1)実験概略図

上の電磁石と下の電磁石は直列に接続しました。吸引力と反発力の切り替えは下の電磁石のコイルの接続を逆にして行いました。
交流と直流の場合で測定しました。
下の写真は実験に使用した電磁石と磁束検知コイルです。
(2)実験結果
実験は、隙間を変えた実験以外すべて交流で行いました。
隙間:5mm (交流)

吸引と反発で同じ電流を流す為に電圧を変えなくてはなりませんでした。吸引の方が高い電圧となりました。反発の場合は磁束が打ち消し合うために、低い電圧で同じ電流が流せるのだと考えています。実際の電圧を下記に示します。
使用したテスターは三和電気計器(株)のPC773のデジタルマルチメーターです。
電流を変えた場合の、吸引、反発時の各部の電圧(交流)
隙間:5mm
交流0.87Aで隙間を変えた場合の比較(交流)

直流0.87Aで隙間を変えた場合の比較(直流)

(3)追加実験結果
吸引力と反発力の比が永久磁石と電磁石では違っていますが、この違いが永久磁石と電磁石の違いによるものか、磁石の形状によるものなのかを調べるため次の実験をしました。
電磁石の吸引力と反発力の比較では、電流を同じにしましたが、そうすると、吸引の時と反発の時では、磁束数が変わってしまいます。交流の場合、電磁石のコイルにかかる電圧で磁束数が決まります。その理由は、コイルに電圧をかけると、コイルにかけた電圧に対抗する電圧が磁束により発生するからです。永久磁石では、吸引時も反発時も磁束数は同じですから、交流の場合も磁束数を同じにして吸引力と反発力を比較しなければならなかったのです。
電磁石の寸法は3cm×3cm×5cmと3cm×3cm×7cmですから、永久磁石の場合も磁石をこの寸法に近づけるために、3cm×3cm×0.1cmと 3cm×3cm×0.5cmの永久磁石を2枚ずつ用意し、これを電磁石の鉄芯に吸引させました。下記はその略図です。

磁石単体での実験は1.(1)の実験と同じです。磁石を鉄芯に吸引させての実験は2.(1)の実験と同じです。
交流0.87Aで吸引力を測定しそのままの電圧で反発力を測定した

永久磁石3cm×3cm×0.1cm単体での実験結果

永久磁石3cm×3cm×0.5cm単体での実験結果

永久磁石3cm×3cm×0.1cmを電磁石の鉄芯に吸引させての実験結果

永久磁石3cm×3cm×0.5cmを電磁石の鉄芯に吸引させての実験結果
-は手持ちの計りでは測定できなかった所です。

反発力%の比較表

永久1t単体:永久磁石3cm×3cm×0.1cm単体
永久5t単体:永久磁石3cm×3cm×0.5cm単体
永久1t鉄芯:永久磁石3cm×3cm×0.1cmを電磁石の鉄芯に吸引させたもの
永久5t鉄芯:永久磁石3cm×3cm×0.5cmを電磁石の鉄芯に吸引させたもの
電磁石同電圧:交流でコイルにかけた電圧を吸引時と反発時で同じにした場合
電磁石同電流:交流でコイルの電流を吸引時と反発時で同じにした場合
電磁石直流:直流でコイルの電流を吸引時と反発時で同じにした場合
直流の場合電圧から磁束数は計算できませんが、交流の場合と同じで、
反発時の磁束数は吸引時の磁束数より少ないものと思っています。
反発力%比較のグラフ

永久Φ40単体:1.(5)の実験結果です。この場合の隙間は5、10、20
30mmです。
その他は反発力%の比較表と同じです。この場合の隙間は5、15、30,45mmです。永久Φ40単体の隙間と同じではありませんが、空白の所はグラフが滑らかになるように、数値を入力しました。―の所も入力しました。
電磁石直流はグラフに載せていません。
3.電磁石による隙間なし、および隙間あり吸引力実験
(1)実験概略図
上の電磁石: 鉄芯:3cm×3cm×5cm高さ
巻数:300回
下の電磁石: 鉄芯:3cm×3cm×7cm高さ
巻数:400回
磁束検知コイル 巻数:100回
カウンターウエイトを決め、スライダックで電圧を徐々に下げ、電磁石が離れた時の電圧でスライダックの電圧を固定し、カウンターウエイトを外し、電磁石を接続し、電磁石のコイルの電圧と磁束検知コイルの電圧を測定しました。
(2)交流・直流隙間なし実験結果
電流の( )内は直流電流です。直流の場合は、吸引力と電流だけの測定です。そして、吸引力が606gの場合は電磁石が1辺だけの接触となっても吸引力が維持されていたので、それ以下での実験はしませんでした。

磁束密度―吸引力 測定値と計算値の比較グラフ

計算力は、計算吸引力で、磁石と磁石の間に蓄積されるエネルギーから計算する方法
P=B2S/(2×μ0)(N) P:計算吸引力
で計算したものです。磁束密度は磁束検知コイルのものを使いました。
電圧から磁束密度を計算する式は下記の通りです。
Vt=ーN×dΦt/dt=ーN×d(Bt×S)/dt=―N×S×dBt/dt
Bt=Bmax・sin(ωt)として
=-N×S×Bmax・sin(ωt)/dt
=-N×S×Bmax・cos(ωt)・ω
電圧VはVtの2乗平均で、実効値と呼ばれています。実効値とは、電気のパワー=電流×電圧=電流×(電流×抵抗)=電流2×抵抗=電圧×(電圧/抵抗)=電圧2/抵抗 から来ています。電流はItは、Imを最大電流として、
It=Im×sin(2・π・f・t) (fは周波数です)
で変化しますが、パワーは電流の2乗に比例するので、実効の電流として2乗平均の平方根を電流の値しているのです。又、パワーは電圧の2乗にも比例します。電気パワーが電流や電圧の2乗に比例しているのと同じように、吸引力は磁束密度の2乗に比例します。ですから、
V=ーN×S×B×ωとして良いと思います。
しかし、力は (Bt)2=(Bmax・sin(ωt))2に比例して変化しているのですが、力の平均はどうなるのでしょうか。交流でも直流でも同じ電流なら、吸引力が、実験ではおおよそ同じであり、計算吸引力が実験値と近い値なので、速度や高さのように普通の平均で良いのだと思います。
V=―N×S×B×ω より
B=-V/(N×S×ω)
Nはコイルの巻き数です。ω=2×π×f で、fは電源の周波数です。ここは埼玉県なので50Hzです。Sは電磁石の面積で単位はm2です
(3)交流隙間あり実験結果
交流電流0.87Aと1.7Aで隙間を変えた場合の、吸引力、各部の電圧と磁束密度

磁束密度の単位はWb/m2です。
平行の計算吸引力の計算で使用した磁束密度は、電磁石間の中間に磁束検知コイルをセットし同コイルの電圧より計算しました。磁束密度は、電圧を(コイルの巻き数×2πf)で割り、更に、これを磁石の面積で割った値です。fは周波数です。ここは埼玉県で50Hzです。
計算式
平行: 吸引力=B2・S/(2・4・π・10-7)×102 (g)
102はニュトンNをgに換算するものです。1N=102gです。
計算に使った磁束密度は磁束検知コイルのものです。磁束検知コイ
ルを通過する磁束は、直線的に、上の磁石と下の磁石につながって
いると思うからです。
単極: 吸引力=m1・m2/((4・π)2・10-7・h2)×102(g)
m1:下コイルの磁束密度×磁石面積
m2:上コイルの磁束密度×磁石面積
h:磁石間の距離 (m)
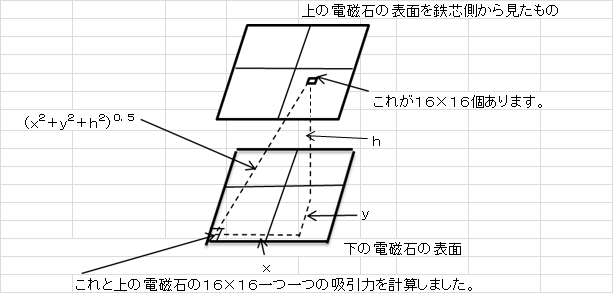
分割:上の磁石も下の磁石も16×16に分割し、分割したものを単極として
計算したものです。磁束密度に分割した面積をかけたものが単極の
磁石の強さWbですが、上と下の電磁石それぞれの磁束密度を使用しま
した。実際にはエクセルを使用して計算しました。下の磁石を4分割
し、8×8個の単極とし、これの一つ一つと上の磁石の16×16個の
単極一つ一つに対する吸引力の垂直分の合計を計算し、これを4倍し
ました。
吸引力=m1・m2/((4・π)2・10-7・)×K×102 (g)
K=(1/(x2+y2+h2))・(h/(x2+y2+h2)0.5)
=h/(x2+y2+h2)1,5
Kの説明図
磁束検知コイルの%
磁石間の中央の磁束検知コイルを通る磁束の、下の電磁石から上の電磁石に届く磁束に対する比率を計算しました。下の電磁石から上の電磁石に届く磁束は上の電磁石の電圧から計算される磁束と考えて良いと思います。下の磁石と上の磁石と磁束検知コイルの内面積は同じですから、磁束の比較は磁束密度で計算しても良いので、比率は磁束密度から計算しました。
4.磁界中の電流に発生する力
(1)磁界中に電流が流れている時の磁力線
電流:直流200A(2A/回×100回) 電線直径:1cm
電流の流れは上から下へで、磁場の方向は時計回転です。
磁界の電磁石:寸法は3cm×3cm、間隔は5cm、350回巻きのコイルに
1Aの電流、磁場方向は左から右
磁界中で電流が流れた時の磁力線です。 電流だけの磁力線です。
電線には手前に動く力がかかります。 磁化されて磁界が少し残っています
磁界だけの磁力線

後日磁束が強め合う側からの写真を撮りました。
条件が少し変わっています。導線の電流は2A×100巻=200Aですが、磁界の方は550巻の0.8Aと変わっています。
磁界中の電流が作る磁力線 電流だけの磁力線

(2)磁界中の電流が発生する力の説明
磁界中で電流が流れた時の磁力線では、電線の上側では、磁界と電流の磁力線が同じ方向です。下側では、反対方向です。ここでも、磁石の反発の実験同様に、磁力線の打消し合いが起こっているのだと思います。16歳の時に磁界中の電流にかかる力を習いましたが、その時の教科書には、次のようにありました。「磁界の磁力線と電流の磁力線は一方で強めあい、反対側では、弱め合うので、電線を動かす力が発生する」と有りました。
磁界中の電流の磁力線の写真を見ると、電線の左側では、磁力線が電線を避けるように上の方に向かっていることが分かります。右側では、電線の上から下側に向かっているのが分かります。分かり易く図にすると下の図のようになります。

磁界の磁力線は上の図のように曲がり、直線になろうとして、力が発生するのだと思います。私は、磁力線は荷電粒子のリングだと考えているわけですから、荷電粒子のリングのつながりから、磁界中の電流に発生する力も説明しなくてはならないと思っています。只今、考え中です。
5.実験考察
電磁石間の隙間がない場合は、ネルギーの蓄積から計算する吸引力の値は実験値に近いものです。隙間20mmは、実験値の90%と100%です。この時、下の磁石から上の磁石に届く磁束の内、磁束検知コイルを通るのは30%ですが、分担する吸引力は
90%以上です。
下の写真は、吸引力実験に用いた電磁石で、隙間20mm、直流電流0.87Aの磁力線です。右側が400回巻電磁石、左側が300回巻電磁石です。

左から右に届く磁束の内磁束検知コイルを通過する磁束は30%にもかかわらず吸引力の分担が90%以上というのは、直線の磁束の吸引力の強さを物語るものだと思います。磁石と磁石の間は20mmですが、この間の磁束は、ばねと同じように、20mmのどの部分でも同じ吸引力が働いているのだと思います。この磁束を形成する、回転する荷電粒子の輪は、20mmの方向では互いに引き合っていることになります。また、磁石の距離が離れると磁束検知コイルを通る磁束が少なくなることは、20mmの隙間方向に直角な面では、隣り合う磁束は反発することを示しているのだと思います。
磁束をばねみたいなものと考えると、磁束1本当たりの吸引力が気になります。吸引力は、P=B2S/(2×μ0)(N) ですが、これを磁束数で割ると、磁束1本当たりの吸引力が計算できます。磁束1本当たりの力をpとすると、p=B/(2×μ0)(N)となり、磁束1本当たりの吸引力は、磁束密度に比例します。ですから、磁束密度の大きい中央の力分担が大きくなるのだと思います。そして、この性質はどこからくるのか考える必要があります。
また、磁石の反発力の吸引力に対する割合は、磁石間の距離が短いほど小さくなりますが、これは、磁石間の距離が短いほど上の磁石と下の磁石の磁束が打消し合う割合が多いことを示しているものだと思います。
隙間なしの吸引力実験で考えたことがあります。磁石の表面が完全な平面となり、磁石と磁石が鉄どうしの接触となった場合、吸引力はどうなるのかということです。吸引力の計算式では、吸引力は透磁率に反比例しますから、磁石と磁石が鉄どうしの接触になると、透磁率は鉄の透磁率となり真空の約5000倍になりますから、吸引力は
1/5000になります。平面の精度を上げてゆけば、鉄どうしの接触面積が増え、高い透磁率の部分が増えれば、吸引力も下がるはずです。実験してみないとわかりませんが、私には、吸引力は変わらないように思えるのです。
6.鉛板を挟んだ場合の吸引力と反発力の変化確認実験
磁力、電気力が光の粒子の交換で説明する理論があります。磁気力は磁力線が元の形に戻る力、電気力は電気力線が元の形に戻る力、重力は、重力線が元の形に戻る力だと考えている私にはこの理論が気になります。γ線、x線、を遮断する鉛板を磁石間に置いたら、磁力はどうなるのか知りたかったのです。ネットの「鉛のx線・放射線に対する特性(MESCO三井金属エンジニアリング)」によれば、鉛に対するガンマ線の透過率は、鉛の厚さ2.5cmで約0.1です。磁石と磁石の間に厚さ2.5cmの鉛板を挟めば、磁力は1/10になるはずです。光を通さないことは、鉛を通しては何も見えないので分かります。ネットで調べると、テレビやラジオの電波も通さないとありました。実験は、磁石と磁石の間に3mm厚さの鉛板を10枚挟んで行いました。電磁石と永久磁石で実験しましたが、吸引力、反発力も変化はありませんでした。
(1)電磁石での実験

上の電磁石: 鉄芯:3cm×3cm×7cm高さ
巻数:400回
下の電磁石: 鉄芯:3cm×3cm×5cm高さ
巻数:300回
鉛板:20cm×20cm×3mm×10枚
実験結果

反発力は吸引力の1/20以下でしたので実験はしませんでした。
(2)永久磁石での実験
ドーナツ型永久磁石 外形:28 mm 内径:10 mm 厚さ:3.5mm

実験結果
吸引力の場合は、鉛がある時も無い時も3gでした。
反発力の場合は、鉛がある時も無い時も4gでした
永久磁石3cm×3cm×0.5cmを電磁石の鉄芯に吸引させての追加実験結果
ただし、磁石間の隙間は52mmです。
吸引力の場合、鉛がある時も鉛がない時も202gでした。
反発力の場合、鉛がある時も無い時も166gでした。
お知らせ
変圧器の実験もしています。変圧器では磁気のない所で発電が起こっています。変圧器の磁気は鉄芯を通るのが殆どで、コイルの所は鉄芯の1/5000以下の磁気です。2次コイルを鉄芯から1mぐらい離した場合の発電の確認実験をしました。2次コイル1巻でも実験しています。興味のある方はお手数でも、変圧器とベクトルポテンシャル、の検索をお願います。
下記が実験の一部です。
6(2)変圧器の発電
変圧器は鉄芯とコイルで出来ています。鉄芯は額縁のようになっています。コイルは二つあります。1次コイルと2次コイルです。1次コイルに交流電圧をかけると2次コイルに、1次コイルと2コイルの巻き数比に比例した電圧が発生します。磁束は鉄芯の中にあり、コイルの所にはありません。ですから、発電機の場合ようにコイルの導線が磁束を横切ることはありません。コイルの所に有るのはベクトルポテンシャルだけです。従って、変圧器の発電は、ベクトルポテンシャルの時間的変化で起こっているのだと考えるしか有りません。つまり、E=δA/δt が起こっているのです。納得の為、下の写真の実験をしました。単巻き変圧器の実験では、巻き数比の電圧が出ました。額縁鉄芯実験では、上部のグリーンテープの所が5cm長さのピースになっているため漏れがあり、巻き数比の7から8割の電圧しか出ませんでした。

上の写真中に丸いものが4個ありますが、これは方位計です。この方位計を使って単巻き変圧器の磁気の影響範囲を調べました。単巻変圧器には0.5Aの直流電流を流しました。因みに発電測定の実験時に単巻変圧器に流れる電流は、0.15Aです。方位計の針が動かない単巻変圧器からの距離は、方位計を単巻変圧器の巻き線と平行にした場合は10cm、直角の場合(下の写真の配置)も10cmでした。直径1mの巻き線のおおよそ85%は単巻き変圧器の磁気の影響が無い所となります。
単巻変圧器と方位計の配置

6(3)単巻変圧器の1回巻2次コイルの部分電圧の測定

上の写真のように、単巻き変圧器に針金を1回通しました。直径は約1mです。電圧は0.39Vでした。針金の抵抗は1.74Ω、電流は0.22Aでした。単巻き変圧器の1次巻き線数は概算で240回です。100V/240=0.42Vですから、0.39Vは大体巻き数比の電圧です。電流も0.39/1.74=0.22で計算通りでした。針金をリングにし、1/10の長さの電圧を計ると、どこも大体0.039Vでした。ベクトルポテンシャルはおおよそ単巻き変圧器からの距離に半比例しますから、発電電圧は単巻き変圧器から遠いほど低いはずです。測定した電圧が電圧降下マイナス発電電圧ならば、場所によって測定電圧は変わるはずですが、どこも同じ測定電圧でした。どういう理由なのかは分かりません。
7. ついでの話
(1)積分
ついでに、積分も考えてみます。積分を習ったのは18歳の時ですが、その時の数学の教科書には、適当な曲線がx軸と作る面積は、終わりと始めの積分値で決まる、とあったのですが、これが理解できませんでした。「適当な曲線で出来る面積が、どうして、始めと終わりの条件で決まるのか」と思ったのでは、理解できる訳がありません。適当な曲線ではないのです。次からの式があるのです。式と言っても簡単です。四則演算による定積分の証明です。面積をSとして、
S=f(x1)・⊿x+f(x2)・⊿x+f(x3)・⊿x
+・・・+f(x n)・⊿x
ここで
f(x1)=(F(x2)-F(x1))/⊿x
f(x2)=(F(x3)-F(x2))/⊿x
f(x3)=(F(x4)-F(x3))/⊿x
・
・
・
f(xn)=(F(x(n+1))-Fxn)/⊿x
代入します。
S={(F(x2)-F(x1))/⊿x
+(F(x3)-F(x2))/⊿x
+(F(x4)-F(x3))/⊿x
・
・
・
+(F(x(n+1))-F(xn))/⊿x}⊿x
S=F(x2)-F(x1)
+F(x3)-F(x2)
+F(x4)-F(x3)
・
・
+F(xn)-F(x(n-1))
+F(x(n+1))-F(xn)
S=F(x(n+1))-Fx1
微分積分を作ったのはニュートンとライプニッツですが、二人はどうしたのでしょうか。解説書によれば、二人は当然のこととし証明は必要としなかったようです。ニュートンは加速度、速度、進んだ距離を計算するために微分積分を作ったのだと思いますから、速度は加速度の積分、進んだ距離は速度の積分ですから、積分が当たり前だったのは分かりますが、ライプニッツはどうなのでしょうか。面積や体積を求めることから積分を作ったのだとすれば、球の体積は球の面積の積分、円の面積は円周の積分ですから、これも当たり前だったのでしょう。
ネットで見ると、きちんとした証明はありましたが、この理解の方法は見つかりませんでした。多分、知ってはいるのでしょうが、格好悪いから誰も書かないのでしょうね。同じことはピタゴラスの証明にも言えるようです。
2018年9月追加
英文で検索してみました。proof of definite integral で検索すると Any proof for the definition of the definite integral の中の #8 March 30,2004 Nate TG に次式がありました。
f(x0) ≒{F(x1)-F(x0)}/(x1-x0) 私の自分のための追加
(x1-x0)f(x0) ≒F(x1)-F(x0)
n-1 n-1
Σ(xi+1-xi )f(xi)≒Σ{F(xi+1)- F(xi)}
n=0 i=0
But it’s easy to see that the sum on the right hand side collapses into:
F(xn)-F(x0)
(2)ピタゴラスの定理
何十年も前に「ピタゴラス」という本を立ち読みしましたが、この本には、「多分、相似の法則での証明が最初で、面積が同じであることを直接証明したのは、その後であろう」とありました。又、ネットの「ピタゴラスの定理とその証明 So-net」では、「相似の法則による説明はアインシュタインによるものと言われている」とありました。
私は、中学の時に、習ったのですが、その時は作図で面積が同じであることを直接証明する方法でした。この方が相似の法則を使うより格好が良いから、指導要領に盛らなかったのかもしれませんね。
(3)浮力の発見
もうひとつあります。アルキメデスの浮力の原理の説明です。アルキメデスは風呂に入っていて浮力の原理を発見し、「分かった」と叫んで、風呂を飛び出した、と言う話を聞いた記憶がありますが、風呂での出来事から浮力を説明する方法は聞きませんでした。今、ネットで見ると、沢山ありますが、どれも「風呂に入るとお湯があふれる」ことから説明しています。私のは少し違います。風呂に入ると水位、いやお湯位が上がります。お湯が持ち上がったのです。当然、もち上がったお湯の量は私の身体の体積と同じです。そして、このお湯は私の体を押し上げています。ですから、その分私の体は軽くなります。当時、色々調べたら、戦前の教科書にはこの説明があったことが分かりました。
(4)一筆書き
一筆書きが出来るか出来ないかの問題はオイラーが解いていますが、一目で分かる方法があります。一筆書きは1本のロープで書くことです。ロープの作る交差点の線の数は始点と終点以外では偶数です。始点と終点が同じ交差点にあれば、どの交差点も偶数です。奇数の交差点は、始点のある交差点と終点のある交差点だけです。従って奇数の交差点が3個以上では、ロープでは作れません。そして、一筆書きでも書けません。
(5)ネットの「宇宙の最初の光を探る」からです。
宇宙では、ビッグバンの時に作られた光が全方向から飛んで来ています。これを人工衛星で観測すると、光の周波数分布は2.726°Kの黒体放射であることが分かっています。
この光には、双極子非等方性があり、180°違えて光の周波数を比較すると周波数の違いが最大になる方向があります。周波数の違いは、地球のある銀河系が、宇宙背景放射に対して、動いているためです。この周波数の違いから、地球がある銀河系が、360Km/Sで赤経11.2時、赤緯―7°の方向に動いていることが分かります。
(6)黒体放射
鉄をガスレンジの炎の中に入れて置くと、赤くなってきますが、これは鉄の温度が上がり、その温度で決まっている光を放出するからです。この光は一つの周波数ではなく、たくさんの周波数の光です。温度によってその周波数分布が決まっていて、その式もあります。周波数分布は元素によらず温度だけで決まっています。
黒体放射は温度によって決まっている光の分布ですが、元素には、元素によって決まっている光もあります。これは、元素の電子がその軌道を変える時に出す光です。元素が熱せられて、電子が、エネルギーの低い軌道から高いエネルギーの軌道に移り、電子が元の軌道に戻るときに、軌道のエネルギーの差分に相当する光を放出するのです。そして、軌道のエネルギー差分で決まる一つの周波数の光だけを放出するのです。

赤経、赤緯は、上の図で、地球を太陽の位置に置き、地球の春分位置に東経0度を合わせ、地球の緯度と経度を空間に広げたものです。北極と南極を結ぶ延長線が赤緯90度です。北極の延長線が赤緯+90度で、南極の延長線がー90度です。赤緯は、春分の位置を0時にして、夏至の位置は6時、秋分の位置は12時、冬至の位置は18時です。
(8)太陽系が動いている方向と公転面からのずれ
太陽系が動いている方向は赤経11.2時、赤緯―7°です。赤経では、秋分の位置の少し前の方向に動いています。赤緯は―7°ですが、公転面に対しては何度になるのでしょうか。太陽系の動く方向が公転面の拡張面上にあれば、地球の公転によるドップラー効果の差は最大になります。赤緯は秋分の位置の少し前で11.2時ですから、赤緯―7は公転面の近くになりますが、もう少し詳しく知りたい所です。

11.2時は秋分の位置から0.8時です。1時は90°/6=15°ですから、0.8時は、15°×0.8=12°です。上の図で太陽の位置から夏至の位置までの距離をrとします。上の図で太陽から11.2時までの距離はr×sin12=r×0.208です。ですから、11.2時の、夏至の位置の23.4°に当たるものは、23.4×((r×0.208)/r)=4.9°です。ですから、公転面の赤緯は―4.9°です。従って、太陽系の移動方向は赤緯―7°ですから、公転面からのずれは、7°―4.9°=2.1°となります。
(9)地球の公転を利用して太陽系の移動速度の観測可能性
太陽系の移動度=360Km/S
地球の公転速度=29.8Km/S
地球の自転速度=0.417Km/S
地球の公転速度は、宇宙背景放射の観測による太陽系の移動速度の約8.3%ですから、地球の公転速度を検出するためには、宇宙背景放射の観測精度より一桁高い精度が必要です。現在の観測精度が1Km/Sを検出できるなら問題ありませんが、どうなのでしょうか。10Km/Sは出来ていそうに思いますので、30±5Km/Sの検出は可能なのではと思っています。
(10)二つの観測で太陽系の移動速度が一致したら
地球の公転速度から太陽系の移動速度を求める時に観測する光は、宇宙背景放射ではなく、太陽系の移動方向にある星の光です。
その星の光の真空中の周波数=f0
太陽系の移動速度=Vx
地球の公転速度=v
光の速度=c
Vx+v の時の地球で観測する周波数=f+
Vx-v の時の地球で観測する周波数=f―
f+=f0×(1+(Vx +v)/c)×(1-(Vx+v)2/c2)―0.5
f-=f0×(1+(Vx -v)/c)×(1-(Vx-v)2/c2)―0.5
この二つの式よりVxとf0が計算できます。そして、Vxが宇宙背景放射から計算された太陽系の移動速度360Km/Sと一致し、地球上での黒体放射にも双極子非等方性があった時、360Km/Sは宇宙背景放射に対するものではなく、真空に対するものだと言えるのではないでしょうか。
2018年9月追加
また、太陽系の移動方向にあるf0が異なるどの星に対しても、Vxが同じであれば、「Vxは真空に対する速度である」と言い切れる思いがします。
(11)地球上での黒体放射にも双極子非等方性があるのではないか
宇宙背景放射が黒体放射であれば、地球上の黒体放射にも同じように双極子非等方性があるのではないでしょうか。同じ黒体放射ならその発生源も同じだと思いたくなります。そして、それは真空だと思います。
鉄の塊といえども、原子の内部はガラガラです。原子の大きさは10-10mで、原子核の大きさは10-15mのですから、原子の内部は真空だらけと言えます。鉄の原子の温度が上がれば、原子内部の真空の温度も上がるはずです。
真空にはベクトルポテンシャルがあったり、磁気の吸引力があったりするのですから、真空は何らかの構造をもっているはずです。真空が何らかの構造をもっているのなら、真空にも黒体放射があるのでないでしょうか。地球上で黒体放射の双極子非等方性が観測されればその証拠になります。宇宙背景放射の双極子非等方性が観測できるのなら、地球上での黒体放射の双極子非等方性も観測できるのではないでしょうか。(9)の二つの観測による太陽系の移動度が一致し、地球上での黒体放射にも双極子非等方性があったら、宇宙背景放射は真空の黒体放射とも考えられますが、どうなのでしょうか。
.
.